杂交随机数

题目附件：

from Crypto.Util.number import bytes_to_long  
  
def lfsr(data, mask):  
    mask = mask.zfill(len(data))  
    res_int = int(data, base=2)^int(mask, base=2)  
    bit = 0  
    while res_int > 0:  
        bit ^= res_int % 2  
        res_int >>= 1  
  
    res = data[1:]+str(bit)  
    return res  
  
def lcg(x, a, b, m):  
    return (a*x+b)%m  
  
flag = b'moectf{???}'  
  
x = bin(bytes_to_long(flag))[2:].zfill(len(flag)*8)  
l = len(x)//2  
L, R = x[:l], x[l:]  
b = -233  
m = 1<<l  
  
for _ in range(2025):  
    mask = R  
    seed = int(L, base=2)  
    L = lfsr(L, mask)  
    R = bin(lcg(int(R, base=2), b, seed, m))[2:].zfill(l)  
    L, R = R, L  
  
en_flag = L+R  
print(int(en_flag, base=2))  
# en_flag = 4567941593066862873653209393990031966807270114415459425382356207107640

这道题其实没有什么考点，我在构思时只是想试试把不同的算法思想混合到一起，于是有了这么一个“四不像”的"加密"结构（之所以打引号，是因为它没有用到密钥，不算是一个完整的加密结构）

本题的意义在于引导新生去自行搜索了解lfsr和lcg这两种流密码拓展一下视野（毕竟这次moectf里大部分密码题都是公钥密码范围的），但实际解题并不需要用到相关的攻击技巧，只要你能看懂python代码就可以解出来😎

下面我将分两个part来进行阐述，如果您只打算了解怎么解这道题的话可以只看 part 1，我会在 part 2 里写一些我的发散思考（不一定正确）

Part 1 题解

观察题目可知，flag被均分成了左右两半：L和R，在每一轮中，分别用旧的R来更新L、用旧的L来更新R，然后将左右互换，再接着进行下一轮，总共进行了2025轮

解密的思路很显然，从最后一轮倒着往前还原，还原2025轮后得到flag

需要注意的是，每一轮倒推的过程中，由于难以给原加密函数找一个逆函数（也许有这么一个函数，但对于比赛来说研究这个问题性价比太低），所以我们需要“猜测”可能的结果，这就涉及到暴力枚举了：
在第 $i$ 轮中，已知 $L_{i}$ 和 $R_{i}$ 的可能值，倒推 $L_{i - 1}$ 和 $R_{i - 1}$ 的可能值
对于每一对可能的 $L_{i}$ 和 $R_{i}$ ， $L_{i - 1}$ 相当于将 $R_{i}$ 左移一位，只有最高位是不确定的，所以分别计算最高位为0或1情况下的 $L_{i - 1}$ 和相应的 $R_{i - 1}$ （反向推导lcg： $R_{i - 1} = 233^{- 1} (L_{i - 1} - L_{i}) (\mod l)$ ），然后检验算得的结果是否满足 $l f s r (L_{i - 1}, R_{i - 1}) = L_{i}$ ，如果满足，就允许其进入下一轮的运算，如果不满足，就将其抛弃。2025轮后，我们最终会得到很多个可能值，从中筛选moectf{前缀找到flag

事实上，在用lfsr检验两种情况时，如果其中一种情况不满足，那么另一种也一样不满足条件；如果其中一种满足，那么另一种也同样满足条件

证明如下：
设 $L_{i}, R_{i}$ 已知，则
$L_{i - 1 (0)} = 0 << (l - 1) + L_{i} >> 1 = L_{i} >> 1$
$L_{i - 1 (1)} = 1 << (l - 1) + L_{i} >> 1 = 2^{l - 1} + L_{i} >> 1$
$R_{i - 1 (0)} = 233^{- 1} (L_{i} >> 1 - L_{i}) (\mod l)$
$R_{i - 1 (1)} = 233^{- 1} (2^{l - 1} + L_{i} >> 1 - L_{i}) (\mod l) = 2^{l - 1} + R_{i - 1 (0)} (\mod l)$
已知进行lfsr得到的新比特值 $b i t = R_{i} [- 1]$
分别对两种情形进行检验
$b i t_{(0)} = ⨁_{i \in L_{i - 1 (0)}, R_{i - 1 (0)}} i$
$b i t_{(1)} = ⨁_{i \in L_{i - 1 (1)}, R_{i - 1 (1)}} i = ⨁_{i \in L_{i - 1 (0)}, R_{i - 1 (0)}} i = b i t (0)$
可知若 $b i t = b i t (0)$ ，自然有 $b i t = b i t (1)$ ；若 $b i t! = b i t (0)$ ，则 $b i t! = b i t (1)$

解题脚本如下：

from Crypto.Util.number import *  
  
en_flag = 4567941593066862873653209393990031966807270114415459425382356207107640  
en_flag = bin(en_flag)[2:]  
l = len(en_flag)//2  
m = 1<<l  
inv = inverse(233,m) 

def single_round(L, R):  
    L0_low = R[:-1]  
    R0_0 = bin(((int(L0_low, base=2)-int(L, base=2))*inv)%m)[2:].zfill(l)  
    R0_1 = bin(((int('1'+L0_low, base=2)-int(L, base=2))*inv)%m)[2:].zfill(l)  
    bit = int(R[-1])  
    R0_0_high = int(R0_0[0])  
    R0_1_high = int(R0_1[0])  
    R0_low = R0_0[1:]  
    b = 0  
    for i in L0_low:  
        b ^= int(i)  
    for i in R0_low:  
        b ^= int(i)  
    L0 = []  
    R0 = []  
    # 根据前面的证明，这里的两个判断条件要么同时成立，要么同时不成立
    if bit^R0_0_high^b == 0:  
        L0.append('0'+L0_low)  
        R0.append(R0_0)  
    if bit^R0_1_high^b == 1:  
        L0.append('1'+L0_low)  
        R0.append(R0_1)  
    return L0, R0  
  
cnt = [0]*2025  
L, R = [en_flag[:l]], [en_flag[l:]]  
for k in range(2025):  
    Ln, Rn = L, R  
    idx = []  
    for i in range(len(L)):  
        Li, Ri = single_round(L[i], R[i])  
        for j in range(1,len(Li)):  
            Ln.append(Li[j])  
            Rn.append(Ri[j])  
        if not Li:  
            idx.append(i)  
            continue  
        Ln[i] = Li[0]  
        Rn[i] = Ri[0]  
    for i in idx[::-1]:  
        Ln.pop(i)  
        Rn.pop(i)  
    cnt[k] = len(Ln)  
    L, R = Ln, Rn  
  
for i in range(len(L)):  
    res = L[i]+R[i]  
    res = long_to_bytes(int(res, base=2))  
    if res[:7] == b'moectf{':  
        print(res)  

print(cnt[-1])  # 查看最终的可能值有多少对
# flag = b'moectf{I5_1t_Stream0rBlock.?}'
# 2560

为了显得学术一点（大嘘），我做了张示意图，这样应该比较直观：

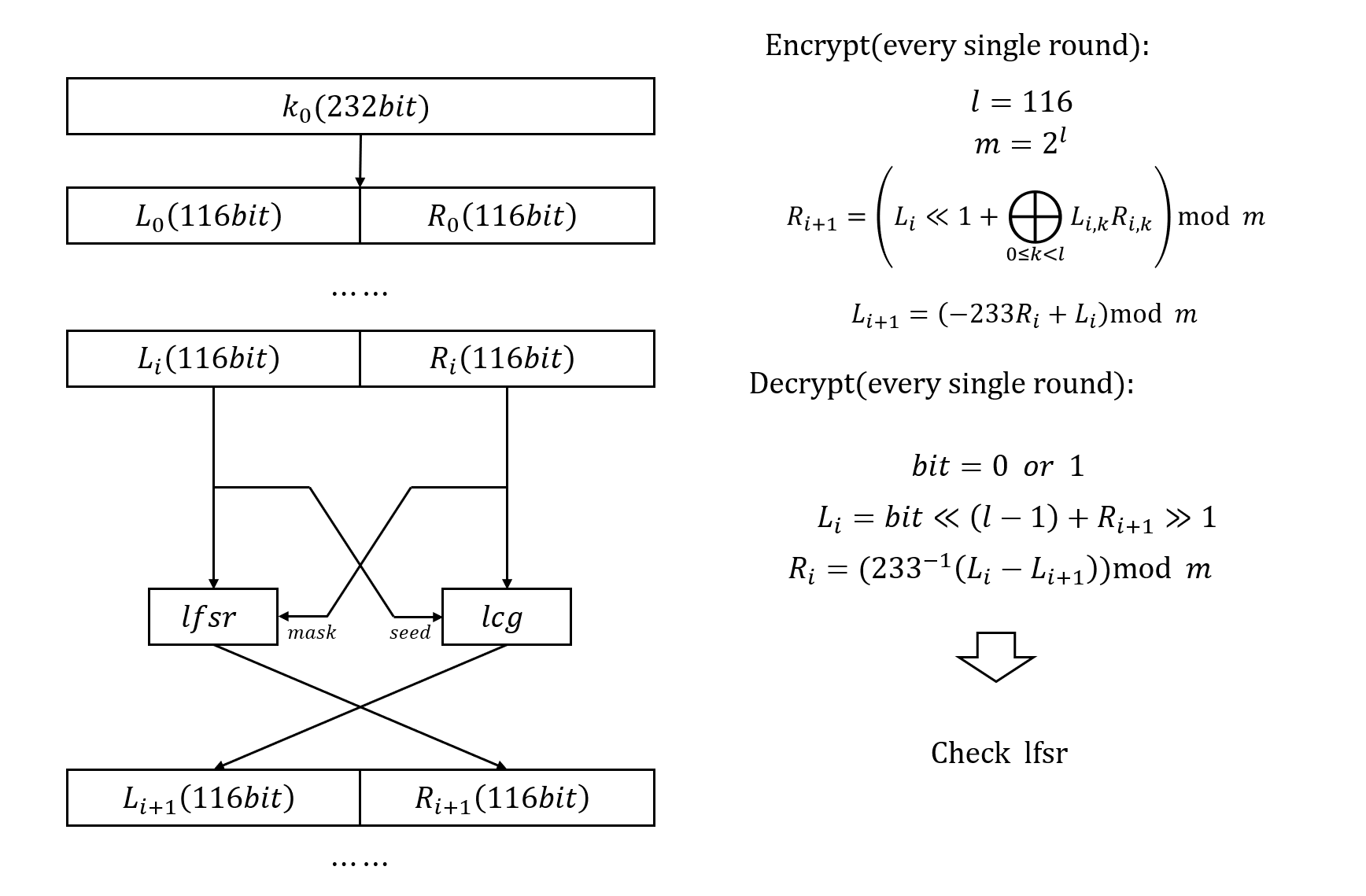
Part 2 抛砖引玉

1

如果你比较爱思考的话，可能会注意到这样一个问题：我怎么确定暴力方法是行得通的呢？
这可是有2025轮啊，如果运气不好、每轮都满足判断条件的话，岂不是最终要遍历非常多次？

从遍历的结果来看，最终flag的可能值只有2560个，遍历搜索的空间并不大
我们可以从概率论的角度来解释：
（由于我自身其实还没学多少概率论，所以就用通俗的话来讲了）

想象一条解密路径，从密文串开始回溯2025个节点（相当于解密2025轮），如果在这条路径上最终到达的终点就是明文串，称这条路径为正确路径，否则则称为错误路径。显然，错误路径有很多，正确路径只有一条。

在某一轮中对一个字符串进行还原，
如果这个字符串所在的路径就是正确路径，那么在这一轮中它会分裂成两个字符串进入下一轮（其中一个在正确路径上，另一个在错误路径上）；
如果这个字符串所在的路径是错误路径，那么我们无法确定它被还原后的表现，它有一定的概率满足判断条件，分裂成两个字符串进入下一轮（两个都在错误路径），或者是不满足判断条件，不进入下一轮，假定这个概率分别是 $\frac{1}{2}$ 。

设还原 $i$ 轮后字符串的数量是 $n_{i}$ ，那么可以算出 $n_{i + 1}$ 的期望值是 $\frac{1}{2} (2 + 0) (n - 1) + 2 = n + 1$
整体上搜索的时间复杂度就是 $Θ (N^{2})$
因此这个搜索范围是可以接受的

这是一位参赛者在🔨里问我的，而且他也详细给出了自己的思考，比我的细致多了。我自己之前没有细想过这个问题（因为我出这道题只是一时脑洞而已，没有做什么研究），经他解答才明白过来，所以非常感谢这位选手🤩

强烈推荐阅读👉某选手wp

2

为啥我把 flag 设置为 Is it Stream or Block? 呢？

~~因为主包学分组密码上头了~~
在每一轮中进行左右互换的想法来自于分组密码里的常见结构。在分组密码里，有很多常用的结构都采用这样的设计，比如 Feistel 结构和 MISTY 结构，不过不同的是我这里将左右交叉了，因此该轮函数是一个难以求逆的单向函数（这也是为什么这个结构不能真正作为一个密码结构）

一个常见的说法是：流密码和分组密码的区别就在于其是否具有记忆性。分组密码内部是无记忆元件的，而流密码内部有记忆元件（记忆元件的意思是这个结构可能受之前的状态值影响）。

从这个角度来看，假如明文非常多，我给它分组处理，而且稍微改变一下本题这个轮函数的结构，在保留流密码设计元素的前提下使得轮函数是一个可逆函数，再在每一轮里加一个与子密钥异或的环节，此时这个结构就可以算是加密结构，那么它应该归为分组密码还是流密码呢？

我认为这得根据分组方式具体是什么再判断。如果是像 ECB 这样将每一组完全分开的模式，那么它应该算作分组密码；但如果是像 CFB 或 OFB 这样利用反馈模式将每一组链接起来的模式，那么它除了使用分组加密的核心算法外，在整体架构上还具有了流密码的特性。